Location: Home >> Detail
TOTAL VIEWS
Crop Breed Genet Genom. 2019;1:e190003. https://doi.org/10.20900/cbgg20190003
1 Ottawa Research and Development Center, Agriculture and Agri-Food Canada, 960 Carling Ave., Ottawa, Ontario, K1A 0C6, Canada
2 Brandon Research and Development Center, Agriculture and Agri-Food Canada, 2701 Grand Valley Road, Brandon, Manitoba, R7A 5Y3, Canada
* Correspondence: Weikai Yan.
This article belongs to the Virtual Special Issue "Genetic Gains in Plant Breeding"
Following successful application in dairy cow breeding, genomic selection (GS) has become a hot topic among plant geneticists and breeders. GS and conventional methods have the same goal of identifying best genotypes for a given crop and region, and should follow the same principles, particularly in dealing with genotype-by-environment (GE). Dealing with GE includes dividing a target region into meaningful mega-environments (MEs) based on repeatable GE patterns and then selecting for each ME. This requires different GS models be developed for different MEs. Selection for each ME requires testing at multiple locations for multiple years to account for the unrepeatable GE in the ME and to estimate the genetic main effect, GP. For a ME with large GE, multiple and diverse cultivars should be selected and recommended. The number of locations, years, and replications within trials required to achieve a certain level of heritability (i.e., selection reliability) for a trait (e.g., yield) can be estimated from existing multi-location, multiyear variety trial data. Instead of direct selection for GP, conventional selections have to resort to indirect selection, negative selection (culling), and a lengthy breeding cycle. GS offers the possibility for direct selection and positive selection for GP and thereby overcoming random GE and shortening the breeding cycle. To achieve this, GS models must be able to predict GP for a breeding population and its prediction accuracy should be measured by r(GM,GP), GM being GS predicted breeding values. This definition of prediction accuracy is the essential connection between GS and phenotype-based selection. This implies that GS models must be developed and evaluated using phenotypic data from multiple locations and multiple years representing the target ME. Using a single training population for model development and a different population for model evaluation will allow estimation of r(GM,GP), but it can be costly and may have limited relevance to a breeding program. A pragmatic GS framework was proposed in this paper, which is to use data from yearly preliminary yield trials for model development, in which a large number of new breeding lines are tested at several locations. A GS model can be developed for each training population-by-trial (location-year) combination, and all available GS models can be used to make predictions, leading to a genotype-by-model two-way table of predictions for the current-year’s breeding population. This table can then be analyzed the way a breeder would do to a genotype-by-environment two-way table of a trait to make selection decisions. This table can also be used to evaluate and select models as a breeder would do for their test environments. Instead of r(GM,GP), “rate of success”, defined as the inverse of the number of genotypes that have to go through yield trials in order to identify a new cultivar, can be used to measure the prediction accuracy of GS. The prediction accuracy or rate of success determines the best pathway to integrate GS into a practical breeding program. GS prediction accuracy is expected to improve with time as more GS models are developed and as the breeding populations and the target ME are better represented in the GS models. A real multi-location, multi-year oat (Avena saliva L.) variety trial dataset and a practical oat breeding program were used to facilitate the discussions.
Genomic selection (GS), originated by Meuwissen et al. [1] and successfully applied in dairy cow breeding [2], has gained much attention among plant geneticists/biostatisticians. GS refers to selection based on predictions from DNA markers densely covering the whole genome, for traits that breeders normally select. This contrasts with traditional marker-assisted selection strategies, which target only traits controlled by a few major genes. Key techniques for applying GS in plant breeding are largely in place, including new marker technologies such as genotyping by sequencing (GBS, reviewed in [3]), bioinformatics tools for handling and analyzing massive sets of markers (e.g., [4,5]), and sophisticated phenotype-genotype modeling methods [1,6–8]. It has been demonstrated by theoretical and empirical studies that GS can be more robust and powerful than previous versions of marker assisted selection and is expected to bring radical changes to plant breeding [9–11]. On the other hand, applying GS in plant breeding can be much more complicated than in dairy cow breeding [12], the most important complication being from genotype-by-environment interaction (GE).
So far, most publications on GS in plant breeding are based on simulations or proof of concept using existing data from historical variety trials, and by researchers other than practical plant breeders. Reports on experimental application of GS have started to appear, e.g., in barley [13], winter wheat [14], and maize [15]. Thus, it seems that GS in plant breeding is now transitioning from theory and technology development to practical implementation. However, there is still a large knowledge gap between genomicists and practical breeders; what seems common knowledge in one discipline may make no sense to the other. This gap must be bridged before GS can be seamlessly integrated into plant breeding programs and achieve its potential. A clear roadmap on how to integrate GS in a practical breeding program remains to be developed. GS is supposed to predict “breeding values”, which is used to make selection decisions. However, this breeding value has not been clearly defined in plant breeder’s terms. From the perspective of plant breeders, the breeding value predicted by GS has to be yield (or any other breeding objective) across a population of environments representing a target mega-environment (ME); it is not just the yield in any environment. This definition is fundamental to developing, testing, and applying GS models in plant breeding.
The overall objective of this article is to set a unified theoretical framework for conventional methods and GS so that genomicists and conventional plant breeders speak the same language when discussing the development, evaluation, and application of GS models in plant breeding. Specific objectives are (1) to review, illustrated with a real crop variety trial dataset, the basic principles of genotype evaluation in relation to dealing with GE, (2) to examine the procedure and selection strategies of a practical oat breeding program in relation to these principles, (3) to outline the potential roles of GS and propose a framework for GS model development, evaluation, and application, and (4) to discuss possible pathways of integrating GS into a practical plant breeding program.
This section summarizes and demonstrates the most important principles in genotype evaluation and selection in plant breeding. These principles apply to both conventional selection and GS and represent a common ground to these two contrasting selection strategies.
A Target Region Should Be Divided into MEs if There Are Repeatable GEA key issue in plant breeding is the presence of GE as discussed abundantly (e.g., [16–18]; and countless publications thereafter), which makes plant breeding much more complicated than dairy cow breeding [7,12], where efforts are made to define and hold constant a single ideal environment. One key step to deal with GE is to separate repeatable GE from non-repeatable GE, conceptually [19] and practically [20–22]. Repeatable GE can be utilized while non-repeatable GE must be avoided. When there is repeatable GE in a target region, the GE patterns should be used as a guide to divide the target region into sub-regions or MEs. Breeding for individual MEs, as opposed to breeding for the whole region, can convert the repeatable GE in the whole region into genotypic main effect (G) within MEs, and thereby maximize breeding progress and overall productivity [21]. For a dataset from multi-year, multi-location trials with some common genotypes across years, GGE-GGL biplot analysis can be used to reveal any repeatable GE, which is the basis for dividing a target region into MEs [20,21,23]. A newer method, location-grouping (LG) biplot analysis, does not require common genotypes across years [22].
In this section the yield data from the 2013 to 2018 Quebec provincial oat trials will be used to demonstrate the principles and methodologies in dealing with GE. Each year, approximately 45 registered oat cultivars or promising breeding lines were tested at nine locations representing the three zones of Quebec [24] plus the Ottawa location in Ontario. A total of 112 genotypes were tested in these six years. Thirteen cultivars were tested in all years, which are currently the primary cultivars in Quebec.
A LG biplot (Figure 1a) provides a graphical presentation of the Pearson correlations among test locations in each of the years (Table 1). Presented in the biplot are the 10 test locations (see their full names in Table 1) and the 57 trials, i.e., location-year combinations (represented by small circles). The biplot reveals two groups of test locations, consistent with results based on the GGE-GGL methodology [20,21]. The group at the lower part of the biplot consists of three Zone-3 locations (Normandin, Hebertville, and Causapscal) and three Zone-2 locations (St. Augustin, St. Etienne, and Princeville). The group at the upper part of the biplot consists of two Zone-1 locations (St. Hyacinthe and St Hugues), a Zone-3 location (La Pocatière), and Ottawa. Ottawa is geographically close to Zone-1 of Quebec. La Pocatière belongs to Zone-3 geographically but often behaves like a Zone-1 location [24]. There is little overlap between the two groups of locations, regardless of the yearly variations in the placement of each location (an indication of genotype by year interaction (GY) and/or genotype-location-year interaction (GLY)); within groups, the locations cannot be separated due to their yearly variations. Hence, Figure 1a revealed two oat MEs, as more clearly shown in Figure 1b. The LG biplot has an interpretation that the cosine of the angle between two trials, two locations, or two groups of locations (i.e., MEs) approximates the genetic correlation between them. Thus, Figure 1a shows that the locations within a group were correlated closely and positively and locations between the two groups were also correlated positively, though loosely (Figure 1a). Consequently, the two MEs, though different, were somewhat positively correlated (Figure 1b).
 Figure 1. Location-grouping (LG) biplot for mega-environment analysis. (a) the LG biplot based on the yield data of the 2013 to 2018 Quebec provincial oat trials; (b) two mega-environments based on (a). This biplot is a graphical approximation of the numerical values in Table 1. See Table 1 for full location names. Each small circle represents a trial (location-year combination).
Figure 1. Location-grouping (LG) biplot for mega-environment analysis. (a) the LG biplot based on the yield data of the 2013 to 2018 Quebec provincial oat trials; (b) two mega-environments based on (a). This biplot is a graphical approximation of the numerical values in Table 1. See Table 1 for full location names. Each small circle represents a trial (location-year combination).
Here we note that the two Quebec oat MEs can be largely (but not completely) explained by geographical regions. However, ME may also be defined by other factors such as crop management (e.g., irrigation) or soil type, or a combination of factors. Regardless of the causes, the key requirement for ME delineation is repeatable GE.
An important principle of dealing with GE is selection for individual MEs, as opposed to selection across MEs. If two MEs are negatively correlated, for example, southern Ontario versus the rest of eastern Canada for oat [25], it will not be possible to select cultivars that are best for both MEs and, therefore, it will be essential to breed and select specifically for each ME. If two MEs are positively correlated, as is in the current example (Figure 1), it may be possible to have cultivars that perform well for both MEs. Nevertheless, there will be cultivars that perform well in one ME but poorly in the other. Thus, selection and recommendation according to ME is still beneficial. This principle also applies to GS; GS models must be developed specific to each ME.
Countless publications and methods exist in the literature on how to identify superior cultivars based on multi-environment trial data, under the name of “stability analysis” (e.g., [26]; all such analyses are meaningful only when applied to selection for a ME; they should not be used across MEs. Discussion hereafter will be restricted to selection for ME1 (Figure 1) in our sample dataset.
Selection for a ME Must Consider both G and GEAnother important principle of dealing with GE is that selection for a ME should consider both mean performance (G) and stability (GE) across environments, and GGE biplot analysis [23,27,28] is a preferred method for this purpose. Selection based on mean performance alone is incomplete use of the information while selection based on stability alone can be misleading; high stability is desirable only when combined with high means, and high stability is least desirable if combined with low means [29]. The yield data of the 13 common cultivars in the 35 trials within ME1 will be used as an example to illustrate genotype evaluation based on multi-environment trial data. These yield data are graphically summarized in the GGE biplot shown in Figure 2. The GGE biplot was based on environment-standardized yield data, as indicated by “Scaling = 2” and “Centering = 1” at the top-left corner of the biplot; it therefore displays only G and GE and explained 53% of the total G + GE. The goodness of fit of the biplot is related to the ratio of G/(G + GE) in the data; a poor fit means a large GE relative to G. A GGE biplot has several functional forms [23,28,30]. The biplot in Figure 2a is the “mean vs. stability” form of the biplot. The red line with a single arrow is referred to as the “average environment axis” (AEA); it passes through the biplot origin and the “average environment” and points to higher mean yield across environments. Thus, the highest yielding cultivars were Nicolas and Akina, and the lowest yielding cultivars were Avatar and Vitality. The six highest yielding cultivars are ranked as Nicolas ≈ Akina > Nice ≥ Kara > Canmore > Richmond. The line with two arrows is perpendicular to (i.e., independent of) the AEA; it points to higher instability in either direction, which means greater contribution to GE. Figure 2a shows that Nicolas and Akina had about the same mean yield but that Nicolas was more stable. Richmond was least stable, as indicated by its long distance to the AEA. None of these high-yielding cultivars was highly stable, indicating large unpredictable GE in ME1.
The “which-won-where” form of the same biplot (Figure 2b) shows which cultivars yielded the highest in which trials in ME1. Akina, along with closely placed Nicolas, was the highest yielder in about half of the trials, which are placed in the sector between the radiate lines labelled 1 and 6. Richmond was the highest yielder in about one-third of the trials, placed in the sector between lines 3 and 4. In these latter trials Nicolas yielded slightly better than Akina. Nice, along with closely placed Canmore, yielded the best in a few other trials, placed in the area between lines 2 and 3. Thus, no cultivar yielded the best in all trials. Consequently, a set of contrasting cultivars (Nicolas, Akina, Nice, Canmore, and Richmond), rather than a single cultivar, should be selected and recommended for ME1, to stabilize the overall production. Selection based on GS predictions must also take this point into consideration. Kara yielded well only in trials where Akina and Nicolas yielded the best; it, therefore, may be omitted from selection/recommendation (Figure 2b).
Figure 2c presents the same biplot but is used to visualize the relative yield of a cultivar, here Nicolas. The single arrowed line pointing to Nicolas passes through the biplot origin and the placement of Nicolas; it shows the relative performance of Nicolas in different trials; it shows that Nicolas yielded better than average in all trials but a few (CAUS3_17 and NORM3_17).
The discussion related to Figure 2 demonstrates that GGE biplot is a versatile tool for genotype evaluation based on multi-environment data. Among other things, it can show both mean yield and stability of the genotypes (Figure 2a), the winning genotypes in each of the environments (Figure 2b), and the performance of a genotype in individual environments (Figure 2c). Moreover, it can show the typical behavior of a “superior” cultivar in a ME, which provides guidance on how to select a superior cultivar. Specifically, Figure 2a shows that Nicolas was overall the best yielder in ME1; Figure 2b shows that Nicolas was not the highest yielder in many of the trials; Figure 3c shows that Nicolas yielded above the average in all trials but a few. Therefore, the best cultivar for a ME does not have to be the highest yielder in every trial; however, it has to yield higher than average in all or most of the trials. On the other hand, a cultivar yielded the best in a single trial or in some trials is not necessarily the best cultivar for the ME. Consequently, a single trial may be used in negative selection (culling inferior genotypes) but cannot be used in positive selection (selection for superior genotypes).
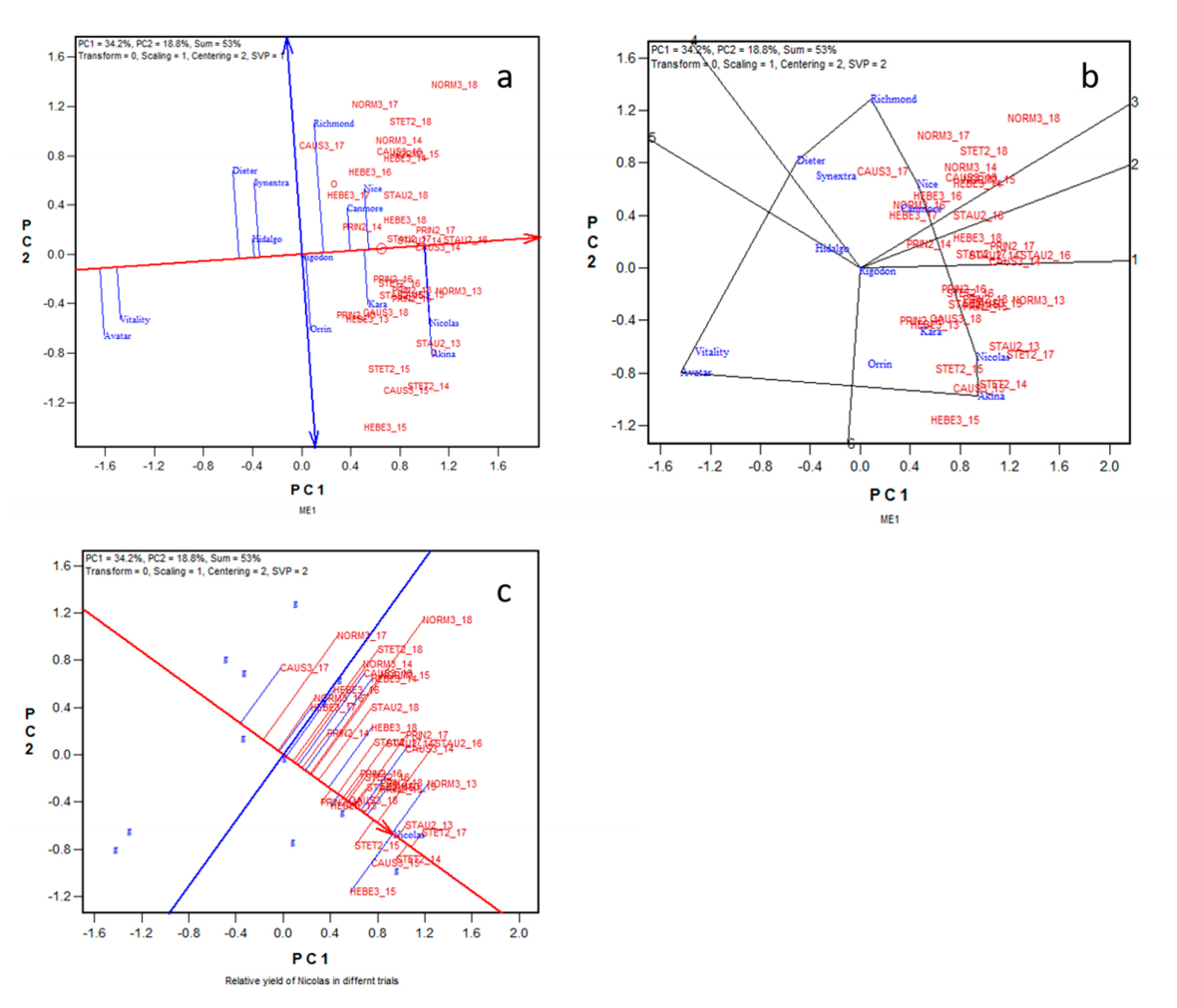 Figure 2. GGE biplot to summarize the yield data of 13 oat cultivars in 35 trials in ME1. (a) The mean-vs.-stability form of the biplot to show the mean yield and stability of the genotypes across trials; (b) The which-won-where form of the biplot to show the highest yielding cultivars in various trials; (c) The biplot form to visualize the relative yield of a genotype, here, Nicolas, in different trials. See Table 1 for full location names.
Figure 2. GGE biplot to summarize the yield data of 13 oat cultivars in 35 trials in ME1. (a) The mean-vs.-stability form of the biplot to show the mean yield and stability of the genotypes across trials; (b) The which-won-where form of the biplot to show the highest yielding cultivars in various trials; (c) The biplot form to visualize the relative yield of a genotype, here, Nicolas, in different trials. See Table 1 for full location names.
Stability across years is important for cultivar selection and recommendation, because the GE within a ME is usually dominated by GY and/or GLY. In ME1, Akina and Nicolas were the highest yielders (when viewed across locations) in years 2013 to 2017 while Richmond was the highest yielder in 2018 (Figure 3a). As a result, Nicolas and Akina were higher yielding and more stable than Richmond (Figure 3b). Nice and Canmore were stable across years but always yielded lower than Nicolas and Akina. Comparison between two cultivars in stability is meaningful only when they have similar levels of mean yield. So cultivar recommendation for ME1 should be in the order of Nicolas, Akina, Nice, Canmore, and Richmond, as shown in Figure 3b. Figure 3c shows the relative yield of Nicolas in different years; Nicolas yielded very well in 2013 and 2015 but not as well in 2018. Nevertheless, it yielded clearly higher than average in all years.
Thus, Figure 3 shows the typical behavior of a superior cultivar across years. Figure 3b shows that Nicolas was the highest yielder in ME1 across years; Figure 3a shows that it was not the highest yielder in all years; and Figure 3c shows that it yielded higher than average in all years. Therefore, the highest yielding cultivar for a ME does not have to yield the best in all years but it has to yield above the average in every year. On the other hand, a cultivar that yielded the best in one year is not necessarily a good cultivar across years. Consequently, superior cultivars have to be identified through multi-year test; multi-location trials in a single year, though more powerful than a single trial, can and should only be used in culling inferior genotypes.
 Figure 3. The genotypic main effect plus genotype by year interaction (GGY) biplot ME1. (a) The which-won-where form of the biplot to show which cultivar yielded the highest in each year; (b) the mean-vs.-stability form of the biplot to show the mean and stability of the cultivars across years; (c) the relative performance of Nicolas in each of the trials.
Figure 3. The genotypic main effect plus genotype by year interaction (GGY) biplot ME1. (a) The which-won-where form of the biplot to show which cultivar yielded the highest in each year; (b) the mean-vs.-stability form of the biplot to show the mean and stability of the cultivars across years; (c) the relative performance of Nicolas in each of the trials.
The discussion associated with Figures 2 and 3 have already demonstrated the principle that adequate testing at multiple locations for multiple years is essential for reliable genotype evaluation. This section defines “testing adequately” in both qualitative and quantitative terms. By definition, the GE within a ME is random and cannot be utilized, and this complicates genotype evaluation. Its adverse effects on genotype evaluation must be minimized through testing at multiple locations for multiple years to fully represent the population of environments in the target ME [17,31]. Within a target ME, the observed value, i.e., the phenotypic value for a trait of interest, P, is a mixture of environmental effect (E), G, and GE, plus non-random variation (i.e., spatial patterns, S) and random errors within trials (ε):

Because the population of environments is defined by both locations and years, genotype evaluation must be conducted under the multi-location, multi-year framework [31]. In this framework, E is partitioned into effects due to location (L), year (Y), and year by location interaction (YL). Consequently, Equation 1 is expanded to:
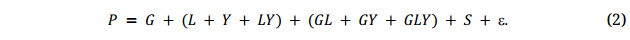
While the purpose of plant breeding is to select G, only P can be determined directly, thus the term “phenotype-based selection (PS)”. This G may be denoted as GP hereafter, standing for breeding values obtained through phenotyping, as opposed to GM, which stands for breeding values predicted by DNA markers. To obtain proper estimation of GP, all the confounding effects in Equation 2 have to be removed; this is achieved by testing at multiple locations for multiple years, and with proper replication and spatial variation adjustment within trials:
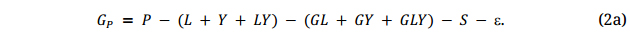
Since GY and GLY usually dominate GE within a ME (if GL dominates GE, then the region would be divided into different MEs), multi-year testing is crucial for identifying truly superior genotypes. From Equation 2 and the analyses exemplified in the previous section, it is obvious that data from a single trial or from multiple locations in a single year may have limited value in identifying superior genotypes. For the same reason, GS models based on data from a single trial or from multiple locations in a single year have limited credibility.
The reliability of the trials for genotype evaluation is measured by the achieved heritability (H) [21,32,33], assuming proper handling of any spatial variations within trials:
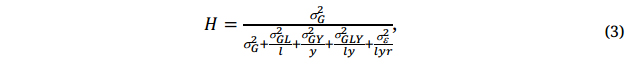
where σx2 is the symbol for various variances specified by the subscript x. An H = 1.0 means the selection would be completely reliable, no matter how small the genotypic difference is; an H = 0 means the selection would be ineffective, no matter how large the varietal difference may appear. Different traits are intrinsically different in H, due to the difference in the number of loci involved in controlling the trait (see also discussion on training population size in relation to Equation 10 later). H is associated positively with the genetic variance (σx2) but negatively with the variances for various components of GE and experimental error. For a given trait, a given set of genotypes (i.e., a breeding population), and a given ME, these various variances are constant (though unknown), and H can only be improved by increasing the number of locations (l), the number of years (y) in which the trials are conducted, and/or the number of replications (r) within trials, again assuming proper handling of spatial variation within trials. Therefore, genotypes must be adequately tested for reliable selection, which is another key principle.
The reliability of the genotypic ranking, as shown in the GGE biplots (Figures 2a and 3a), which is measured by H, increases with increased test locations and years and replications within trials (Equation 3). However, each additional trial or replication comes with a cost. Both selection reliability and selection cost must be considered in a practical breeding program. A compromise between the two is to target H = 0.75 [23,25]. The optimum number of years, the optimum number of locations per year, and the number of replications within trials can all be roughly estimated by:
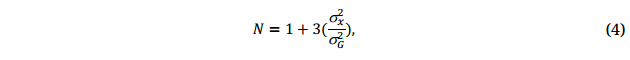
Where σG2 and σx2 are the estimated genetic variance and GE variance or genotype by replication variance, respectively, depending on the scenario.
The officially recognized crop variety registration committees in Canada (possibly in other countries as well) require at least two or three years of multi-location testing and a minimum number of location-year combinations to decide if a breeding line can be supported for registration; experience indicates that a three-year multi-location testing is usually adequate for identifying superior cultivars. Applying Equation 4 to the genotype by year two-way tables (not presented) in our sample dataset, the number of years required to achieve an H = 0.75 was estimated to be 2.8 for ME1 and 2.4 for ME2.
Applying Equation 4 to the yearly genotype by location two-way tables (not presented) in our sample dataset, the number of locations required to achieve H = 0.75 for ME1 was estimated to be from 5.4 to 10.2, depending on the year, and averaged 7.2 per year. For ME2, this number was from 1.9 to 6.2, and averaged 4.4. So, the number of test locations actually used (6 for ME1 and 4 for ME2) in the Quebec oat trials were close to be adequate.
When the two MEs were analyzed jointly, the required number of locations per year was estimated to be from 7.0 to 11.9, depending on the year, and averaged 8.6. This number is smaller than what was estimated when the two MEs are analyzed separately (7.2 + 4.4 = 11.6). This suggests that when two MEs are similar, treating them as one may be more efficient in identifying the best genotypes, supporting the conclusion of Atlin et al. [33]. However, analysis across MEs may mask some important patterns between and within MEs. For example, Nice and Canmore were important cultivars in ME1 (Figures 2 and 3) but were among the poorest yielders in ME2 (results not shown).
Increasing the number and diversity of genotypes in the trials in a non-random fashion (i.e., increasing the size and diversity of the training population in terms of GS model development) may increase the genetic variance. As a result, the pre-set heritability level may be achieved with smaller number of locations per year and number of replicates within trials (Equation 3).
Final Selection Decisions Have to Consider Multiple Breeding ObjectivesIn addition to dealing with GE for a given trait, selection based on multiple traits is also an important aspect. Although the economic yield is always the most important trait for all crops, other traits can also determine the fate and value of a genotype. Multiple breeding objectives must be considered in genotype selection and cultivar recommendation, which adds another dimension to the complexity and difficulty in plant breeding. In fact, plant breeding is not only to increase the yield of a crop but more to combine high yield with other desirable traits (i.e., performance reliability and end-use quality). For oat, lodging resistance and test weight are two most important traits, in addition to yield. For oat millers, groat content and beta-glucan content are very important too. The millers also require the oil content to be lower than 8% to meet the requirement for healthy food labeling. In addition, many other traits are also considered by growers and end-users. For convenience, traits can be classified into three functional categories. Type I: yield, the single most important trait; Type II: key traits, which can fail a cultivar for a target environment and/or end-use if a minimum requirement is not met; and Type III: traits that may add value but usually do not fail a cultivar regardless of their levels [34].
Two strategies have been used in dealing with multiple traits in plant breeding: independent culling and index selection, used in tandem or jointly [35]. Independent culling can be conducted any time when a relevant trait is observable or determined; index selection has to wait till data for all target traits become available. Independent culling is to discard a genotype if it does not meet the minimum requirement for any single breeding objective, regardless of its levels in other traits. Index selection is to select genotypes based on an index, which is a linear combination of the levels of the breeding objectives, with each trait being given a weight according to their importance perceived by the breeder/researcher. Linear indices assume that the importance of the level of one trait is independent of the levels of other traits. However, the fact is, the economic value of the level of a trait depends on the associated level of other traits, particularly that of yield. For example, superior lodging resistance is important only if it is combined with high yield; it has little use to growers if it is associated with low yield. Based on this understanding, genotypes should be evaluated on their levels of combining yield with other breeding objectives [36]. One way to do this is to transform a genotype-by-trait two-way table into a standardized genotype by yield*trait (GYT) two-way table. From the standardized GYT table, a GYT index can be calculated, which is the mean across the standardized yield-trait combinations. This GYT index can be used to indicate the overall superiority of the genotypes. Preferably, this standardized GYT table can be visually studied using a GYT biplot [36].
Presented in Figure 4a is the GYT biplot for ME1, based on the 2013 to 2018 Quebec data for ME1 (numerical data not presented). In addition to yield, four traits are included: lodging score, test weight, beta-glucan content, and groat content. The single-arrowed line passes through the biplot origin and the average yield-trait combination; it points toward superiority; the projections of the genotypes onto this line are highly correlated with the GYT index. Thus, the overall superiority of the 13 cultivars was in the order of Nicolas ≈ Akina > Canmore ≥ Kara > Nice… > Avatar. The double-arrowed line indicates the strengths and weaknesses of the cultivars. For example, Figure 4a shows that Akina was stronger than Nicolas in combining yield with lodging resistance and beta-glucan content while Nicolas was stronger than Akina in combining yield with test weight and groat content. Thus, the GYT biplot has two advantages over traditional selection index. First, the GYT index reflects the understanding that the importance of a trait level is dependent on the yield level with which it is associated; second, the GYT biplot is informative in presenting the trait profiles of the genotypes. The GYT biplot is also a useful tool to breeders in selecting breeding parents. For example, Figure 4a is highly suggestive that a cross between Akina and Nicolas, the two best cultivars with contrasting trait profiles, may lead to a promising breeding population for combining all the breeding objectives considered here.
The GYT biplot in Figure 4a assumed equal importance for all yield-trait combinations. This is justified as the biplot also presents the trait profiles of the genotypes, which can be used to make selection decisions based on a specific requirement. For example, if beta-glucan content and/or lodging resistance are considered more important, then Akina, instead of Nicolas, should be recommended; if test weight and/or groat content are more valued, then Nicolas should be more preferred than Akina. Nevertheless, differential weights can be applied to GYT biplot analysis if it is so desired [34]. Figure 4b is the GYT biplot applying more weight to lodging resistance (1.5 times of other traits). As a result, Akina and Kara, which had better lodging resistance, are placed before Nicolas and Canmore, respectively, as compared to Figure 4a. Comparing Figure 4b with Figure 4a indicates that differential weighting is not needed for biplot-based decision making; it is needed, however, if the decision is to be made solely on the GYT index.
 Figure 4. The genotype by yield*trait (GYT) biplot for ME1 to show the overall superiority of the cultivars and their trait profiles in ME1. (a) Equal weights for all traits; (b) a greater weight for lodging resistance (1.5 time of the normal weight). Each yield*trait combination is denoted as Y*Trait. A negative sign (“–”) is placed before “Y*Lodging” to transform “lodging score” to “lodging resistance”. The traits are: beta-glucan content; GROAT: groat content; KG/HL: test weight; LOD: lodging score; BGL.
Figure 4. The genotype by yield*trait (GYT) biplot for ME1 to show the overall superiority of the cultivars and their trait profiles in ME1. (a) Equal weights for all traits; (b) a greater weight for lodging resistance (1.5 time of the normal weight). Each yield*trait combination is denoted as Y*Trait. A negative sign (“–”) is placed before “Y*Lodging” to transform “lodging score” to “lodging resistance”. The traits are: beta-glucan content; GROAT: groat content; KG/HL: test weight; LOD: lodging score; BGL.
To summarize this section, dealing with GE is a key issue in plant breeding, and dealing with GE should follow the following principles and methodologies. First, mega-environment analysis should be conducted to discover any repeatable GE patterns so as to divide the target region into meaningful subregions or MEs. The GGE-GGL biplot or the LG biplot can be used for this purpose. Selection within MEs, rather than across MEs, can make use of the repeatable GE. Data from multi-location, multi-year trials are required for this analysis; the GGE-GGL biplot, or better, the LG biplot, is the recommended tool for mega-environment analysis. Second, selection for a ME should consider both G and GE, and GGE biplot analysis is a versatile and effective tool for this purpose. For a ME with large and unpredictable GE, multiple and diverse cultivars, rather than a single cultivar, should be selected and recommended. Third, testing adequately. That is, the number of test locations, the number of years of testing, and the number of replications within trials should be sufficiently large to achieve a certain level of heritability. These numbers can be roughly estimated from existing crop trial data. Data from a single trial or from multi-location trials in a single year can be used in culling inferior genotypes but are not sufficient for selecting superior cultivars. Finally, ultimate selection decisions have to consider multiple breeding objectives, which adds another dimension to the complexity and difficulty of plant breeding. GYT (Biplot) Analysis can be a useful tool for this purpose. These principles and methods apply to both conventional selection and GS.
So far, most, if not all, crop cultivars are developed primarily through conventional selection methods, and conventional breeding has been successful. Nevertheless, the selection methods used in conventional plant breeding bear little relation to the principles discussed in previous section. In practice, no selection decision is made on data from replicated trials tested at multiple locations for multiple years as required in Equation 2 in most part of the breeding cycle, because this is practically unfeasible. Instead, indirect selection (i.e., selection via presumably correlated traits) and negative selection (i.e., culling for inferior genotypes) are the key approaches in a conventional breeding program. In this section we will describe the procedures and selection methods that we use in the Ottawa oat breeding program. This will set a scene for discussing the advantages and disadvantages of conventional selection versus GS and strategies of integrating GS in the breeding program.
The Breeding ProcedureThe target region of the oat breeding program at AAFC-Ottawa is eastern Canada (including provinces of Ontario, Quebec, New Brunswick, Nova Scotia, and Prince Edward Island); the target end-uses are multifold but milling (food) oat is the main driving factor. Eastern Canada consists of two contrasting oat MEs, southern Ontario and the rest of eastern Canada [25]. Within the second ME, different but similar MEs exist ([20–22], and the previous section). The main breeding objectives include high grain yield, superior lodging resistance, superior grain quality (high test weight and large, heavy kernels, and high groat content), and superior compositional quality (high levels of β-glucan and protein, and an oil concentration lower than 8%). Resistance to crown rust is also critical for oat production in southern Ontario.
The oat breeding cycle can be divided into four stages (Figure 5). Stage 1 is parent selection and hybridisation; this is the first and most important stage in breeding. 50 to 100 crosses are made yearly; usually each cross contains at least one parent that is a proven superior cultivar or promising breeding line. Stage 2 is generation advance, to advance the breeding population (c. 10,000 F2 individuals from all crosses) to a generation when individuals become homozygous enough for effective selection. We grow three generations per year in greenhouses, advancing the population to F4 in one year, or to F7 in two years. This generation advance is performed by modified bulk, which emulated single-seed-descent. No deliberate selection is made during the advance, although unintended selections may occur due to competition among plants and other factors.
Stage 3 is visual selection, which consists of two consecutive years. In the first year (Stage 3.1), approximately 10,000 breeding lines (F4 or F7) are grown into 10,000 hill plots in the field. Visual selection is conducted by eliminating lines that are excessively tall, late, weak, or diseased. Lines not eliminated are harvested and visually examined for grain characteristics (e.g., kernel size, shape, uniformity, plumpness, seed amount, hull thickness, and the feel of test weight). Only lines with seeds thought to be acceptable to oat growers and end-users will be kept. After this year, the 10,000 breeding lines will be reduced to approximately 1000, a 90% reduction. In the 2nd year of visual selection (Stage 3.2), the 1000 lines are grown into 1000 unreplicated plots, each consisting of four rows of 4 m long, referred to as the “Observation Nursery”. These lines are also selected visually similar to the previous year, but the visual judgement for yield potential may be more credible. Uniformity (homozygosity) is also considered at this stage. This nursery also serves to increase the seed for use in next year’s yield trials. After the two years of visual selection, the breeding population is reduced to approximately 300 lines.
Stage 4 is the yield trial stage. It consists of five years of multi-location testing, with reduced number of lines and increased number of test locations and replications each year. In year-1 (“Home Test” or Stage 4.1) the c. 300 lines selected from the previous year are tested at three locations in eastern Canada with two replications each. The lines are evaluated primarily for grain yield but also for grain quality, end-use quality (determined from grain samples from one or two locations), resistance to lodging, resistance to key diseases that occurred, and days to maturity. This is a large-scale test; it is not only costly but also difficult to implement as not many collaborators can accommodate a trial of >600 yield plots (i.e., it is limited by “physical capacity and partnerships”, [37]. Around 60 of the 300 lines will be selected and advanced to year-2 test (“Preliminary Test” or Stage 4.2), which is conducted at c. 10 locations, including six locations in eastern Canada (representing the two contrasting ME) and three or four locations in western Canada. This wide test is to gather information on any specific adaptations of the genotypes to different regions. Approximately 20 of the 60 lines will be selected and advanced to the registration trials (Stages 4.3 to 4.5). The Registration test consists of three years (years 3 to 5), which are required to obtain support for registration in Ontario, Quebec, and Atlantic provinces. In the yearly Registration test, around 20, 10, and five lines are first-, second-, and third-year entries, respectively. The Registration test is conducted at seven eastern Canadian locations covering the two contrasting MEs, with four (officially required in Ontario) or three (in other provinces) replications at each location. This number of locations is smaller than the estimated minimum requirement [25], which may limit the selection reliability. Each year in Stage 4, genotypes are eliminated for low yield, poor standability, or poor end-use quality. Lines that survived all five years of testing may be released as new cultivars. Using these procedures, we were able to release and license over 20 new oat cultivars in the last 10 years, and some of these showed significant improvements over official controls and became leading cultivars in eastern Canada [38,39].
Limitations of Conventional SelectionThe selection theory presented earlier requires that selection be made on data from replicated trials conducted at a sufficiently large number of locations for a sufficiently large number of years so as to remove complications from experimental error, spatial variation, GL, GY, and GLY (Equation 2). However, selection in the practical breeding program rarely meets this requirement. In the visual selection stage (Stage 3), the selection is not even on the target traits as they are not measurable. Instead, the selection is on traits that are observable and thought to contribute to a target trait. Visually assessed yield components are used to select for yield; plant height and perceived straw strength are used to select for lodging resistance; maturity and height are used to select for regional adaptation; and visual grain characters are used to select for grain quality and milling quality. All selections are based on unreplicated observations in a single environment.
In the yield trial stage (Stage 4), direct selection for the target traits becomes possible. However, the most intense selections are made on single year data, and relatively few genotypes are advanced to test for multiple years. The selection is, therefore, confounded with GY and GLY; it may be confounded with GL as well due to the limited number of test locations. Therefore, even at this stage, most selections can be considered as genitive selection, i.e., to eliminate poor genotypes, rather than to select superior genotypes.
So, indirect selection and negative selection (culling) are the key strategies used in conventional selection. The philosophy behind conventional selection is that a superior cultivar should perform well in all environments (all locations and years) for all breeding objectives and their components, and any genotype that is poor in any environment (location or year) for any breeding objective or any of its components should be eliminated. While this philosophy seems logical, it is difficult to implement accurately. In addition to GE, unfavorable associations among traits [38] and pleiotropic gene effects further complicates the selection. For example, late maturity may cause a genotype unfit to some environments but it is difficult to decide how late is too late, as late maturity is usually associated with high yield potential; tall plants tend to be susceptible to lodging but it is difficult to decide how tall is too tall, as taller plants may have higher yield potential in drought-prone environments. Kernel size is a yield component; however, it is difficult to decide how small is too small. In fact, the highest yielding cultivar in eastern Canada, Nicolas (Figures 2–4), is known to have relatively small kernels and to be late in maturity. If selection on maturity and kernel size are too harsh, genotypes like Nicolas may be discarded before they have a chance to show their yield potential. Thus, the danger exists that truly superior genotypes can be discarded during the various stages of culling.
Due to the nature of indirect selection and negative selection, it takes over 10 years to complete a breeding cycle, from making a new cross to planting a new cultivar in farmers’ field (Figure 5). From the “breeder’s equation” (Equation 5, [37,40]), the length of the breeding cycle, L, is a severe limiting factor to breeding progress:
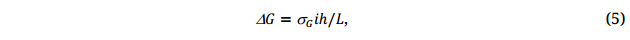
where △G is breeding progress, σG is as defined in Equation 3, i is the selection intensity, h is the selection accuracy, which is equivalent to 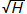 as defined in Equation 3.
as defined in Equation 3.
Despite its limitations, conventional breeding has been successful and cost effective. The Breeder’s Eye, i.e., the art component of plant breeding [41], plays an important role for breeding success. It allows the breeder to make reasonably good decisions with limited cost, time, and information. The greatest advantage of conventional selection is its cost effectiveness. For example, the cost is negligible in the visual selection stage (Stage 3, Figure 5), during which the breeding population is reduced by 97% (a very high selection intensity). Any alternative methods, including GS, have to compete with conventional breeding in cost efficiency.
As an aside to the current discussion on selection but a key issue to plant breeding as a whole, the complete breeder’s equation may be expressed as:
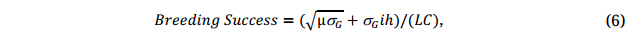
where μ is the mean of the breeding population, and C is the cost involved in the breeding process. The first part of the equation is to create a promising breeding population, and the second part is to select superior genotypes out of it. The breeding value of a breeding population, VP, is determined by both the population mean and the genetic variability within it:
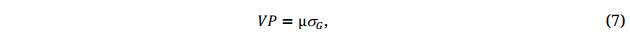
and parent selection (Stage 1, Figure 5) is of utmost importance for breeding success. All factors in Equation 6 should be considered in developing a successful breeding program/selection strategy.
To summarize this section, conventional selection methods are characterized by indirect selection and negative selection. Poor genotypes are culled (rather than superior genotypes selected) on individual target traits or their components in a single environment, a single trial, or multi-location trials in a single year. Genotypes that have survived all these negative selections may be released as new cultivars. Conventional selections are subjective and have a long breeding cycle but are flexible and cost-effective.
In GS, the breeding values of the genotypes in a breeding population, GB.M, are predicted via genetic markers (M)(Equation 8) [6]. M represents allele values of DNA markers densely covering the whole genome so that all possible loci controlling the trait of interest are tagged by markers in high linkage disequilibrium; the parameter b represents the effects of each of the marker alleles on the breeding value.
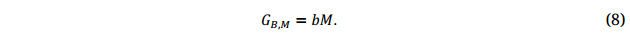
The purpose of plant breeding is to select genotypes that perform best across the population of environments in a target ME (Equation 2a). Therefore, GB,M must be the predicted performance of the genotypes in a breeding population across environments representing the target ME. This definition of GB,M, though common sense to plant breeders and quantitative geneticists, seems to be new to the GS literature. This definition brings PS and GS in the same framework, and has two extremely important implications:
First, the success of GS must be measured by r(GB,M, GB,P), i.e., the correlation between GB,M and GB,P, the latter being the genetic main effects of the genotypes in the breeding population obtained from multi-location, multiyear trials representing the ME (Equation 2a). Therefore, GS prediction accuracy cannot be obtained by testing the breeding population in a single trial or multi-location trials in a single year.
Second, a useful GS model, i.e., the marker effects b, has to be developed by testing the training population(s) at multiple locations for multiple years representing the ME, so as to obtain the genetic main effects of the training population (Equation 2a), GT,P, because
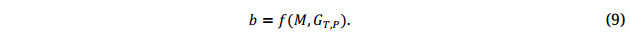
Equation 9 implies that GS model development relies on three aspects: (1) the quantity and quality of marker data (M), (2) the quantity and quality of phenotypic data (GT,P), and (3) the robustness of modeling (statistical) methods (f). Since the first and third aspects have been addressed abundantly in existing literature, this paper focuses on aspect 2.
Assuming sufficiently high prediction accuracy, (i.e., high r(GB,M, GB,P), GS would have two dramatic advantages over conventional selection:
(1)
(2)
The key to GS success is how to achieve high prediction accuracy. Intuitively, Equation 9 may imply that a single GS model is developed by testing a single training population at multiple locations for multiple years in order to obtain the required GT,P. This would mean that a training population has to be developed and tested over multiple years, independently of the trials in a practical breeding program.
A relaxation of this requirement would be to allow the training population to differ each year or even in each trial (location-year combination), as long as each training population sufficiently represents the breeding population(s). This would allow the routinely conducted breeding trials, e.g., the Home Test (Stage 4.1, Figure 5), to be used for model training. A caveat of this is that lines in this population have already been subject to selection; they can provide an effective training set only if contrasting alleles remain present. In our program, we believe that this criterion is fulfilled because the Home Test is composed of visually selected lines as well as lines from GS selected in both positive and negative directions. However, it would not be fulfilled if the Home Test were composed only of lines selected in a positive direction by GS.
Given a set of appropriate training populations, each subjected to replicated testing, a GS model can be developed for each population by location by year combination, so Equation 9 will become:
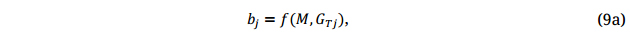
where GTj is the genotypic main effects for the training population(s) tested in trial j, each trial being a location by year combination, and bj the corresponding maker effects.
Accordingly, Equation 8 becomes
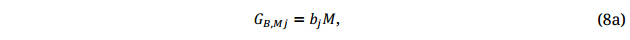
where GBj is the predicted breeding values for the breeding population based on each of all available GS models that have been developed. The results will be a genotype by model two-way table of GS predictions for the trait of interest, similar to the genotype-by-environment data of a trait obtained from multi-environment trials. This genotype-by-model two-way table of GS predictions can be analyzed in the same manner as that breeders would analyse the phenotypic data from multi-environment trials (Figures 2 and 3), replacing environments with models. The final GS decision will be based on the mean and stability of the genotypes in the breeding population across GS models. Moreover, when many models become available, the genotype-by-model two-way table of predictions can be used to evaluate the models based on their representativeness and discriminating ability in the same way that breeders evaluate their test environments [23]; poor models would be discarded and only good models would be used in making decisions. With time, more GS models will be developed, the breeding population and the ME will be better represented, and the GS predictions will be more accurate. Importantly, although three years of testing are required for supporting the registration of a cultivar, GS models from many years may be developed and used in the prediction and selection, which may lead to an H (Equation 3) or h (Equation 5 ) that is higher than any practical multi-location multi-year test system can possibly achieve (Equation 3). This is a unique opportunity provided by GS for accurate selection of superior genotypes. In addition, GS models for multiple breeding objectives have to be developed. Predictions for multiple traits can be integrated by methods such as GYT analysis (Figure 4; [34,36]) to make final selections.
Prediction accuracy is everything. As mentioned earlier, GS prediction accuracy has to be measured by r(GB,M, GB,P), i.e., correlation between marker-predicted breeding values (GB,M) and the genetic main effects of the genotypes (GB,P), of a breeding population for a ME. Since it takes multi-location trials for multiple years to obtain GB,P, decisive evaluation of GS success will also take years. Furthermore, it is costly and unrealistic to test a full breeding population or even the subset of GS selected lines at multiple locations for multiple years merely to fulfil requirements of “experimental validation”. Therefore, instead of determining the prediction accuracy, we propose a “rate of success” to measure the success of a selection strategy. The rate of success is defined as the inverse of the number of genotypes that have to be tested in the yield trials to identify a superior genotype. For example, if one out of 60 GS-selected lines survived the yield tests and met the requirement for new cultivar registration, then the rate of success is 1/60.
It should be pointed out that so far most publications on GS in plant breeding have used the approach of cross validation to assess GS prediction accuracy (e.g., [42]). Cross validation may be useful for assessing the goodness of fit of the GS models developed from different modelling approaches and different training population sizes, but it is not a direct measure of GS prediction accuracy or rate of success. The correlation between GS predicted values and a one-year performance is not a decisive measure, either, due to the presence of large GY and/or GLY (Figure 3), and because it does not fulfil any practical question that a breeder would have about the effectiveness of GS in developing successful plant varieties, unless it is restricted to single well-defined environments (as it is in many animal breeding applications).
Training Population Size Required for GS Model DevelopmentAccording to Daetwyler et al. [43], the potentially achievable GS prediction accuracy, R(GB,,M, GB,,P), is determined by:
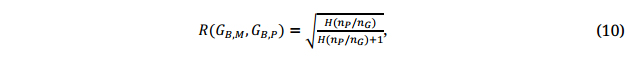
where H is the achieved heritability as defined in Equation 3, nP is the size of the training population, and nG is the number of loci controlling the trait of interest in the breeding population. The achieved prediction accuracy, r(GB,M, GB,P), should be equal to the achievable or potential prediction accuracy, assuming perfect marker data, phenotypic data, and modeling technique (Equation 9).
Equation 10 shows that the potential prediction accuracy of GS can be increased by increasing H and nP and by reducing nG. For a given breeding population and trait, nG is a fixed, though usually unknown, number. Therefore, improvement of the prediction accuracy can only be achieved by two approaches: (1) increasing the size of the training population, and (2) improving the heritability through adequate testing (Equation 3). The combined requirement is phenotypic data from testing a large enough training population(s) at multiple locations for multiple years representing the target ME. This section focuses on the required population size.
The required training population size can be derived from Equation 10 with some assumptions. The relationship between the achievable prediction accuracy R and the ratio nP/nG at two levels of heritability is depicted in Figure 6, based on Equation 10. It can be seen that the achievable prediction accuracy can reach 0.8 or higher when nP/nG ≥ 7, even when the heritability is only 0.25. Assuming that the number of polymorphic loci controlling the trait of interest in the breeding population is 100 (i.e., nG = 100), which should be adequately large for any breeding population and trait (a population of 10,000 allows only 13 genes to segregate in all possible combinations), then a training population of 700 would be sufficient (np = 7 nG = 700) to achieve a potential prediction accuracy of 0.8 at H = 0.25. Assume a heritability of 0.5, which can often be achieved for grain yield in our Home Test (Stage 4.1, Figure 5), and again assume nG = 100, the required training population for a potential prediction accuracy of 0.80 is approximately 3.5nG or 350. This is close to the number of entries we normally test in the Home Test. Assume H = 0.5 and nG = 100 and setting the achievable prediction accuracy to 0.9, the required population size will be nP = 8.0nG or 800. Therefore, a training population of 350 to 800 should suffice to achieve a potential prediction accuracy of 0.8 to 0.9 for any trait and breeding population. It can also be seen that the effect of increasing population size on improving prediction efficiency is diminishing when the population size is beyond 8nG. If nG = 50 is a reasonable assumption, then the required population size is from 175 to 400 to achieve a prediction accuracy of 0.8 to 0.9.
This analysis suggests that data from past trials in which a sufficiently large number of genotypes (e.g., nP ~ 175) were tested may be used in GS model development. Many breeding programs have a test similar to our Home Test (Stage 4.1, Figure 5), which tests approximately 300 lines at several locations each year. Such data can be readily used in GS model development. To bridge the gap between genomic research and practical oat breeding, a joint test among four oat breeding programs in North America (North Dakota State University (Dr. Michael McMullen), University of Saskatchewan (Dr. Aaron Beattie), Agriculture and Agri-Food Canada (AAFC) at Brandon, and AAFC at Ottawa), referred to as ENCORE, was started in 2013. Each year approximately 240 new oat breeding lines from the four breeding programs were tested at five locations (Fargo ND, Saskatoon SK, Brandon MB, Lacombe AB, and Ottawa ON) with two replications each. Data from the Ottawa site have already been used in GS development for eastern Canada. The phenotypic data from the western Canadian locations should be useful for developing GS models for western Canada.
Pathways to Integrate GS in Plant BreedingThere are two potential GS injection points into the breeding stream (Figure 5). One is to start GS before any visual selection (“GS-In1”), and the other is to start GS after the first-year visual selection (“GS-In2”). Some believe that breeder’s visual selection is no better than random and would like to use GS-In1 to avoid loss of useful genotypes by breeder’s culling. However, it is a fact that most lines in the breeding population will eventually be discarded and many defective genotypes can be visually eliminated with confidence and little cost at Stage 3.1. In addition, Stage 3.1 is a stage that cannot be skipped because it is necessary to increase seed and to obtain DNA samples for genotyping even if no visual selection is to be made. If the plants are not grown in “hills” in the field, they will need to be grown in pots in a greenhouse. The former costs less and is potentially more effective and informative. Currently approximately 90% of the initial breeding population is eliminated at Stage 3.1 in our program. To reduce possible loss of useful genotypes, a less stringent visual selection pressure can be implemented. For example, the elimination rate may be reduced to 80%, allowing GS to be applied within the non-culled lines (GS-In2). The cost for genotyping for GS-In2 is only 10–20% of that for GS-In1. Therefore, GS-In2 is considered a more rationale choice at present. GS-In1 may become a viable choice in the future when the cost of GS is dramatically reduced and/or GS prediction becomes extremely accurate. In practice, we are currently testing GS on a small scale (2000 lines per year) using GS-ln1, with the objective of comparing the success rate of GS relative to visual selection at Stage 3.1 without introducing bias of previous selection.
GS-selected lines can be returned to the breeding stream at different points (Figure 5), depending on the GS prediction accuracy. If the rate of success is 1/60, i.e., if 60 GS-selected lines are needed to identify a superior cultivar, then the 2nd year visual selection (Stage 3.2) and the first-year yield trials (Stage 4.1) can be bypassed (“GS-Out1”). If the GS prediction is 1/20 or higher (GS-Out2), then Stages from 3.2 to 4.2 can be bypassed. When the prediction accuracy is extremely high (e.g., 1/2), then Stage 3.2 and all of the yield trials can be bypassed (GS-Out5). The rate of success for our visual selections (Stage 3) is approximately 1/150 to 1/200, considering that we test 200 to 300 lines in the Home Test, and some of the lines are intended to select breeding parents rather than cultivars.
It is relevant here to emphasize the importance of prediction accuracy or selection reliability. The often-cited breeder’s equation (Equation 5) suggests that breeding progress is proportional to the selection intensity and the selection reliability. What has not been emphasized enough in the literature is that the allowable selection intensity is dependent on the selection reliability, and a high selection intensity is justified only when the selection reliability is high enough to allow it. The proposed rate of success may be regarded as an integrated measure of both prediction accuracy and selection intensity. A greater prediction accuracy means a shorter breeding cycle, less test cost, and greater breeding efficiency (Figure 5).
GS predicted lines may also be used as parents to start a new breeding cycle [9,37]. This is feasible only when the GS prediction accuracy or the rate of success is sufficiently high, e.g., >1/10. Also, it should be noted that parents used in a cross should not only have high breeding values but should also be genetically diverse (Equation 7); the breeding value is only one part of the whole picture [44].
Additional comments on the usefulness of bypassing Stages 3.2 and 4.1 by GS follow. Visual selection in Stage 3.2 can be fairly cost effective and there is little economic advantage to bypass this stage with GS. However, visual selection and GS prediction may be used jointly at this stage to make more accurate selections. Bypassing the Home Test (Stage 4.1) would be highly desirable as this is a large, costly test. However, Home Test is needed to generate phenotypic data for GS model development and cannot be bypassed until the time when GS model development is considered complete. It is difficult to tell when such time will come, however. A breeding program has to constantly bring in new germplasm and to address emerging environmental and market challenges. Nevertheless, selection decisions may be made based on both phenotypic data and GS prediction at this stage. As GS prediction becomes more accurate, a greater weight can be placed on GS prediction relative to visual selection.
Current Status of GS Application and Future PlanIn 2016, 40 oat lines were selected prior to Stage 3.2, based on GS models developed on data from the 2015 Home Test and ENCORE conducted at Ottawa. These lines, along with lines visually selected at Stage 3.2, were entered the 2017 Home Test (Stage 4.1); eight of the GS-selected lines were selected and advanced to the 2018 Preliminary Test (Stage 4.2); four of them will be further tested in the 2019 Registration Test (Stage 4.3). In 2017, 60 lines were selected prior to Stage 3.2 based on GS models developed on data from the 2015 and 2016 Home Test and ENCORE at Ottawa. These lines, along with visually selected lines, were entered the 2018 Home Test (Stage 4.1); 14 of these lines were selected and will be advanced to the 2019 Preliminary Test (Stage 4.2). Some of the GS selected lines were also selected visually. In a few years from now, we will be able to see how many of the GS-selected lines will outperform visually selected lines and be qualified to release as new cultivars. These exercises correspond to the “GS-In2→GS-Out1” pathway (Figure 5).
In 2018, 60 lines were selected out of a set of crosses before any visual selection (prior to Stage 3.1), based on GS models developed on phenotypic data from the 2015 to 2017 Home Test and ENCORE at Ottawa. These lines will be compared with 60 visually selected lines from the hill nursery (Stage 3.1), from the same crosses, in the 2019 Home Test. Lines that survive the test will be advanced and further tested. This GS exercise corresponds to the “GS-In1→GS-Out1” pathway (Figure 5). This work will be repeated in the next four years; each year more GS models from more trials will be used.
Importantly, in each of these first few years of selection, GS has been based on models developed by combining one to several field tests at a single test location, Ottawa, in one or two training populations. In future years, we intend to invoke multiple GS predictions from multiple training populations evaluated in multiple environments (locations and years), using the framework described earlier in this paper. GS models will be developed for all available location-year combinations in the Home Test, plus ENCORE at Ottawa, for eastern Canada. Similar work is being done for the oat breeding program at the Brandon Research Development Center, whose mandate is to develop oat cultivars for western Canada. With time, and as more training data (genotypes, environments, and their interactions) are built into the GS models, GS prediction accuracy should increase. Conclusive results on GS rate of success will be obtained in the next few years, which will allow us to decide the best GS pathway(s) (Figure 5).
To successfully integrate GS in a practical breeding program, genomicists and conventional plant breeders must speak the same language, which are the principles of dealing with GE for a trait and unfavorable associations among breeding objectives. An essential link between GS and PS is that the breeding values predicted by GS, GM should correlate with the genetic main effects, GP obtained from multi-location multi-year trials representing the target ME. This link determines what phenotypic data are needed for GS model development and evaluation. Conventional selection methods have to resort to indirect selection, negative selection, and a long breeding cycle to obtain GP; GS offers the opportunity to directly select on GP through GM and thereby to dramatically shorten the breeding cycle. A pragmatic GS framework was proposed for GS model development and application, in coupling with routinely conducted breeding trials. A rate of success was defined to measure the success of GS and visual selections. Possible pathways of integrating GS into a practical breeding program was outlined, and the best pathway is dependent on the prediction accuracy or rate of success of GS.
WY developed the main ideas and drafted the manuscript; NT, WB, JM and JF contributed in discussions that led to some of the ideas, and reviewed, corrected, and proved the final version.
The authors declare no conflict of interest.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
Yan W, Tinker NA, Bekele WA, Mitchell-Fetch J, Fregeau-Reid J. Theoretical Unification and Practical Integration of Conventional Methods and Genomic Selection in Plant Breeding. Crop Breed Genet Genom. 2019;1:e190003. https://doi.org/10.20900/cbgg20190003

Copyright © 2020 Hapres Co., Ltd. Privacy Policy | Terms and Conditions